Skip to contents

Radial zonation in liver lobules

Michael Barkasi

2026-03-13

tutorial_liverradial.Rmd

Introduction

Mammalian liver tissue is organized into concentric rings of cells called lobules. These lobules are filled with capillaries which carry blood to an interior central vein. The rings, or zones, of the lobules are functionally distinct. As Droin et al. (2021) explain, this functional zonation “is accompanied by gradients of gene expression along the portal-central axis, with some genes expressed more strongly near the central vein, and vice versa for portally expressed genes” (p. 43). In addition, “liver physiology is also highly temporally dynamic”, with rhythmic cycles driven by “the complex interplay among the endogenous circadian liver oscillator, rhythmic systemic signals and feeding-fasting cycles” (ibid).

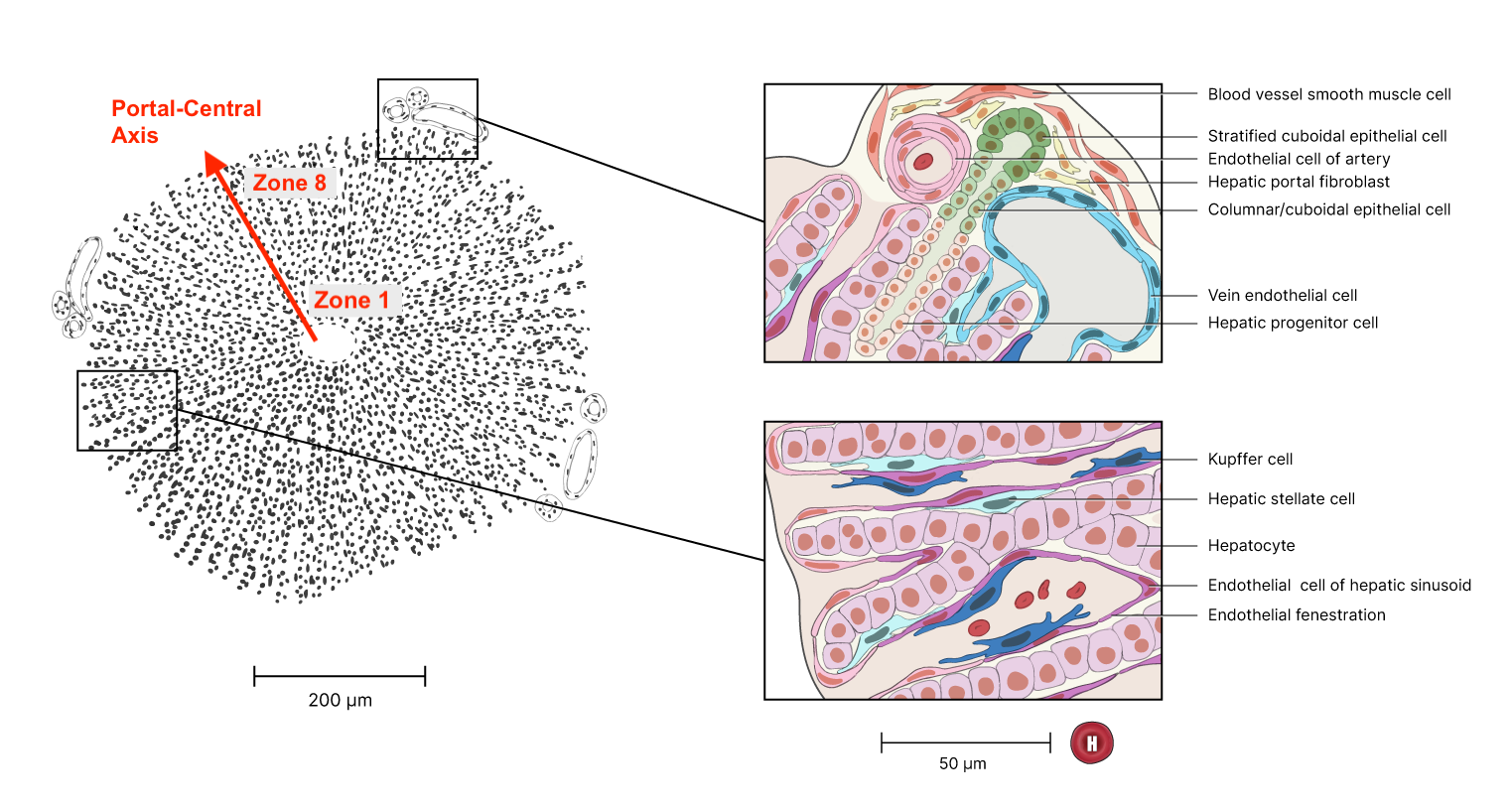
Figure showing the organization of liver lobules

Liver-lobule organization. Red annotation added. Original figure from the Human Reference Atlas. (12/18/2024). Liver Lobule. NIAID NIH BIOART (CC BY 4.0).

Thus, the zonated expression of genes in the liver is a good candidate for functionally relevant spatial gene variation, and hence rhythmic oscillations in gene expression which potentially interact with this spatial variation are good candidates for functional spatial effects (FSE). To investigate this question, albeit not using the jargon “FSE”, Droin et al. used a linear mixed-effects model with second-degree polynomials to represent spatial variation and harmonic terms to represent temporal rhythm. Specifically, after normalizing transcript counts y, they log-transformed those counts: y \mapsto \log_2(y + \Delta) - B such that “the offset \Delta = 1\times 10^{-4} buffers variability in genes with low expression, while the shift B = -\log_2(11\times 10^{-3}) changes the scale so that y=0 corresponds to about 10 mRNA copies per cell” (p. 55). They then modeled the transformed counts y_{x,t,i} for spatial position x, time t, and individual mouse i as: y_{x,t,i} = \mu_i + \mu(x) + a(x)\text{cos}(\omega t) + b(x)\text{sin}(\omega t) + \epsilon_{x,t,i} with: \begin{aligned} \mu(x) &= \mu_0 + \mu_1P_1(x) + \mu_2P_2(x) \\ a(x) &= a_0 + a_1P_1(x) + a_2P_2(x) \\ b(x) &= b_0 + b_1P_1(x) + b_2P_2(x) \end{aligned}

for P_1(x) and P_2(x) the first- and second-degree Legendre polynomials. Statistical testing showing significant coefficients \mu_1 or \mu_2 (terms of pure spatial variation) and a_0 or b_0 (terms of pure temporal variation) would indicate additive spatial zonation and temporal rhythm, while significant coefficients a_1, a_2, b_1, or b_2 (terms for position-dependent temporal variation) would indicate interacting spatial and temporal effects. These model coefficients are, of course, log2 fold changes (L2FC).

Whether or not interaction is required for a FSE, or if instead the combination of additive zonation and temporal rhythm suffices, is a conceptual question we can set aside here. What’s important is that this model allowed Droin et al. to test for FSEs by first:

  • testing for significant model coefficients, then
  • searching for KEGG pathways enriched with genes having these significant model coefficients.

They found enriched KEGG pathways for many of their additive genes. Depending on one’s perspective, this finding is either evidence that temporal rhythm has a FSE, or (if interaction is necessary) evidence that temporal rhythm has no FSE. Either way, their model afforded a principled test for FSEs.

This same analysis can be run with a wisp. Wisp models are, of course, built explicitly for modeling effects on one-dimensional spatial variation, including temporal effects from a time series. While wisp models represent time as a discrete additive effect rather than as a harmonic oscillation (and thus lack a period term \omega which could be used to test for period length), known or expected oscillations can be represented by indexing times to some repeating point in the series (“zeitgeber time”). In this case, effects of circadian rhythms or feed-fast cycles can be modeled by indexing times to the start of each day. (Indeed; even Droin et al. exploited this fact by fixing \omega=2\pi/24\text{ hr}, instead of estimating \omega from the data.)

Processing the data

Droin et al. have made some of their data available in an easily accessible form in a GitHub repo. The data consists of ten MatLab (.mat) files, one for each mouse used in the study. Transcriptome sequencing was performed on each mouse at one of four zeitgeber time points (ZT): 0 hr, 6 hr, 12 hr, and 18 hr. The ZT for each sample is included in the file name. This particular data set was actually generated via bulk sequencing, not with spatial transcriptomics. However, using previously validated marker genes, Droin et al. assigned to each cell a probability of zone membership, for each zone along a discrete one-dimensional axis of eight liver portal-central zones (the Pmat matrix). These probabilities were then multiplied by normalized count values for each gene in each cell (the mat.norm matrix) and log-transformed using the transform shown above.

It would not be a good idea to reconstruct this data and give it to the wisp() function directly. Wisp is intended to model raw counts from Poisson processes, meaning positive integers without weighting or normalization. The concern raised by weighting and normalization is that wisp parameters are fit by maximizing the likelihood of the data, under the assumption that the data comes from a gamma-distributed Poisson process. Data may no longer fit this distribution after it has been weighted or normalized.

Hence, instead of reconstructing the Droin et al. data directly, we will use it to simulate raw counts suitable for wisp modeling. For each cell with normalized pseudo-count y and probabilities p_1,\ldots,p_8 of membership in zones 1 to 8, counts will be drawn from the Poisson distribution, for i=1,\ldots,8: y_i\sim \text{Pois}(y\times 1\text{e}3) The multiplication by 1\text{e}3 is to denormalize the pseudo-count to a realistic expression rate. Next, draws are made from a binomial distribution b_i\sim \text{Binom}(1, p_i) Finally, for each zone i, a cell is added to the data with count y_ib_i.

First, we load the MatLab files:

library(R.matlab)
files <- list.files(path = "Droin_data", pattern = "\\.mat$", full.names = TRUE)
Droin_data <- lapply(files, readMat)
names(Droin_data) <- basename(files)

Droin et al. bulk-sequenced thousands of genes. For this demonstration, we will model just a few with zonation and temporal rhythm:

Abbreviation Name Zonation Rhythm
GLUL Glutamine synthethase Central
ASS1 Urea cycle gene argininosuccinate synthetase Portal
ARNTL, BMAL1 Basic helix-loop-helix ARNT like 1 Circadian
DBP PAR bZip transcription factor Circadian
ELOVL3 ELOVL fatty acid elongase 3 Central Circadian
PCK1 Phosphoenolpyruvate carboxykinase 1 Portal Circadian

We can subset the data as follows:

# List of genes to keep
genes_to_keep <- c("glul", "ass1", "arntl", "dbp", "elovl3", "pck1")

# For each loaded MatLab file, subset to the above genes
for (fn in basename(files)) {
    # Check that the desired genes are in the file
    gene_idx <- which(unlist(Droin_data[[fn]][["all.genes"]]) %in% genes_to_keep)
    genes_to_keep <- unlist(Droin_data[[fn]][["all.genes"]])[gene_idx]
    # Subset file components to just these genes
    Droin_data[[fn]][["seq.data"]] <- Droin_data[[fn]][["seq.data"]][gene_idx,]
    Droin_data[[fn]][["mat.norm"]] <- Droin_data[[fn]][["mat.norm"]][gene_idx,]
    Droin_data[[fn]][["MeanGeneExp"]] <- Droin_data[[fn]][["MeanGeneExp"]][gene_idx,]
    Droin_data[[fn]][["SE"]] <- Droin_data[[fn]][["SE"]][gene_idx,]
    Droin_data[[fn]][["q.vals"]] <- Droin_data[[fn]][["q.vals"]][gene_idx,]
    # Rename data rows with gene names
    rownames(Droin_data[[fn]][["seq.data"]]) <- genes_to_keep
    rownames(Droin_data[[fn]][["mat.norm"]]) <- genes_to_keep
    rownames(Droin_data[[fn]][["MeanGeneExp"]]) <- genes_to_keep
    rownames(Droin_data[[fn]][["SE"]]) <- genes_to_keep
    names(Droin_data[[fn]][["q.vals"]]) <- genes_to_keep
    Droin_data[[fn]][["all.genes"]] <- genes_to_keep
  }

Finally, we can build a data frame of simulated counts suitable for the wisp() function. As described in more detail in the tutorial on modeling the laminar cortical axis, wisp expects a data frame with the same structure used by well-known R functions for linear modeling, such as lme4::lmer() or stats::lm(). Each row should be a cell, with columns for the count, spatial coordinate (bin), RNA species (gene), random variable (mouse), and any fixed-effects (in this case, ZT).

# Create count_data frame for use with wisp()
count_data <- data.frame()

# For each subsetted MatLab file ...
for (i in seq_along(Droin_data)) {
  
  # Grab gene list and data dimensions
  gene_list <- rownames(Droin_data[[i]][["mat.norm"]])
  n_genes <- length(gene_list)
  n_cells <- ncol(Droin_data[[i]][["mat.norm"]])
  n_bins <- ncol(Droin_data[[i]][["Pmat"]])
  
  # Grab row sums for renormalization of probability to 1
  Pmat_row_sums <- rowSums(Droin_data[[i]][["Pmat"]])
  
  # De-normalize transcript counts to realistic rates
  denormalized_rates <- Droin_data[[i]][["mat.norm"]] * 1e3
  
  # ... for each gene
  for (g in c(1:n_genes)) {
    
    # ... for each zone (i.e., spatial coordinate, or bin)
    for (b in c(1:n_bins)) {
      
      # Simulate count of gene g in each cell, for mouse i
      sim_gene_counts_by_cell <- rpois(n_cells, denormalized_rates[g,])
      
      # Get probability of bin membership for each cell, for mouse i 
      probability_of_zone_membership_by_cell <- Droin_data[[i]][["Pmat"]][,b] / Pmat_row_sums
      
      # Randomly select whether each cell is in this bin
      cell_weight <- rbinom(n = n_cells, size = 1, prob = probability_of_zone_membership_by_cell)
      
      count_data <- rbind(
        count_data,
        data.frame(
          # add mouse number
          mouse = rep(i, n_cells),
          # extract ZT from file name and add
          ZT = rep(as.numeric(gsub("\\D", "", names(Droin_data)[i])), n_cells),
          # add bin number
          bin = rep(b, n_cells),
          # add gene name
          gene = rep(gene_list[g], n_cells),
          # compute and log-transform the zone-weighted normalized gene counts
          count = sim_gene_counts_by_cell * cell_weight
        )
      )
      
      # Note: to reconstruct the Droin et al. data, use: 
      #       count = transform_data(Droin_data[[i]][["mat.norm"]][g,] * Droin_data[[i]][["Pmat"]][,b])
      #   with the function: 
      #       transform_data <- function(x) {
      #           log2(x + 1e-4) - log2(11e-5)
      #         }
      
    }
  }
  
}

Fitting a wisp

For the purpose of this tutorial, the above preprocessing code is not run. Instead, the simulated data is saved to a CSV file available with this package. We will load it directly.

count_data <- read.csv(
  system.file(
      "extdata", 
      "Droin_radial_count_data_sim.csv", 
      package = "wispack"
    )
  )

The first step is to set the variables to be modelled:

data.variables <- list(
  count = "count",
  bin = "bin", 
  context = "liver", 
  species = "gene",
  ran = "mouse",
  timeseries = "ZT"
)

There are only eight coordinates in the spatial dimension (bins 1 to 8). Ideally we would have more, but we can compensate by adjusting the model settings. Potentially needed adjustments include lowering buffer_factor (which controls minimum distance between rate-transition points), LROwindow_factor (which controls the range of rate-transition slopes detected when searching for rate-transition points), and LROcutoff (which controls the sensitivity of rate-transition point detection). Previous testing (not shown here) suggests that all that’s necessary is lowering the LROcutoff from the default 2.0 to 1.5.

model.settings <- list(
  LROcutoff = 1.5
)

Next, we need to adjust a few of the plot settings. First, we want to print plots selectively at the end, so print.plots is set to FALSE. Second, count_size and count_jitter are adjusted to account for the low number of spatial coordinates. Finally, we adjust the alpha values to focus on the fixed-effect predictions rather than the random-effect predictions.

plot.settings <- list(
  print.plots = FALSE,
  title_size = 14,
  log.scale = TRUE,
  count_size = 2.5,
  count_jitter = 0.0,
  count.alpha.none = 0.8,
  count.alpha.ran = 0.5,
  pred.alpha.ran = 0.0
)

Finally, we can fit the model. For the purpose of estimating the parameters, we will use bootstraps instead of MCMC sampling. So, we set the number of MCMC steps to zero and the number of bootstraps to 1000.

# Load wispack
library(wispack, quietly = TRUE)

# Set random seed for reproducibility
ran.seed <- 123
set.seed(ran.seed)

# Fit model
radial.model <- wisp(
  count.data = count_data,
  variables = data.variables,
  bootstraps.num = 1e3,
  max.fork = 10,
  model.settings = model.settings,
  MCMC.settings = list(MCMC.steps = 0),
  plot.settings = plot.settings
)
## 
## 
## Parsing data and settings for wisp model
## ----------------------------------------
## 
## Model settings:
##  buffer_factor: 0.05
##  ctol: 1e-06
##  max_penalty_at_distance_factor: 0.01
##  LROcutoff: 1.5
##  LROwindow_factor: 1.25
##  rise_threshold_factor: 0.8
##  max_evals: 1000
##  rng_seed: 42
##  warp_precision: 1e-07
##  round_none: TRUE
##  trtKO: none
##  inf_warp: 450359962.73705
## 
## Plot settings:
##  print.plots: FALSE
##  dim.bounds: 
##  log.scale: TRUE
##  splitting_factor: 
##  CI_style: TRUE
##  label_size: 5.5
##  title_size: 14
##  axis_size: 12
##  legend_size: 10
##  count_size: 2.5
##  count_jitter: 0
##  count.alpha.ran: 0.5
##  count.alpha.none: 0.8
##  pred.alpha.ran: 0
##  pred.alpha.none: 1
## 
## MCMC settings:
##  MCMC.burnin: 100
##  MCMC.steps: 0
##  MCMC.step.size: 0.5
##  MCMC.prior: 1
##  MCMC.neighbor.filter: 1
## 
## Variable dictionary:
##  count: count
##  bin: bin
##  context: liver
##  species: gene
##  ran: mouse
##  timeseries: ZT
##  fixedeffects: ZT
## 
## Parsed data (head only):
## ------------------------------
##   count bin context species ran timeseries
## 1     0   1   liver   arntl   1          0
## 2     0   1   liver   arntl   1          0
## 3     0   1   liver   arntl   1          0
## 4     0   1   liver   arntl   1          0
## 5     0   1   liver   arntl   1          0
## 6     0   1   liver   arntl   1          0
## ----
## 
## Initializing Cpp (wspc) model
## ----------------------------------------
## 
## Infinity handling:
## machine epsilon: (eps_): 2.22045e-16
## pseudo-infinity (inf_): 1e+100
## warp_precision: 1e-07
## implied pseudo-infinity for unbounded warp (inf_warp): 4.5036e+08
## 
## Extracting variables and data information:
## Found max bin: 8.000000
## Fixed effects:
## "timeseries"
## Ref levels:
## "0"
## Time series detected:
## "0" "6" "12" "18"
## Created treatment levels:
## "ref" "6" "12" "18"
## Constructed weight_row matrix
## Context grouping levels:
## "liver"
## Species grouping levels:
## "arntl" "ass1" "dbp" "elovl3" "glul" "pck1"
## Random-effect grouping levels:
## "none" "1" "10" "2" "3" "4" "5" "6" "7" "8" "9"
## Total rows in summed count data table: 2112
## Number of rows with unique model components: 264
## 
## Creating summed-count data columns and weight matrix:
## Random level 0, 1/11 complete
## Random level 1, 2/11 complete
## Random level 2, 3/11 complete
## Random level 3, 4/11 complete
## Random level 4, 5/11 complete
## Random level 5, 6/11 complete
## Random level 6, 7/11 complete
## Random level 7, 8/11 complete
## Random level 8, 9/11 complete
## Random level 9, 10/11 complete
## Random level 10, 11/11 complete
## 
## Making extrapolation pool:
## row: 38/192
## row: 76/192
## row: 114/192
## row: 152/192
## row: 190/192
## 
## Making initial parameter estimates:
## Extrapolated 'none' rows
## Took log of observed counts
## Estimated gamma dispersion of raw counts
## Estimated change points
## Found average log counts for each context-species combination
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Estimated initial parameters for fixed-effect treatments
## Built initial beta (ref and fixed-effects) matrices
## Initialized random-effect warping factors
## Made and mapped parameter vector
## Number of parameters: 324
## Constructed grouping variable IDs
## Size of boundary vector: 1848
## 
## Estimating model parameters
## ----------------------------------------
## 
## Running bootstrap fits
## Checking feasibility of provided parameters
## ... no tpoints below buffer
## ... no NAN rates predicted
## ... no negative rates predicted
## Provided parameters are feasible
## Initial boundary distance (want > 0): 0.206765
## Performing initial fit of full data
## Penalized neg_loglik: 1044.51
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: Context: liver, Species: dbp
## liver, Species: arntl
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: Context: liver, Species: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## ass1Context: liver, Species: elovl3
## Context: liver, Species: glul
## 
## Context: liver, Species: pck1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: arntl
## Context: liver, Species: elovl3
## Context: liver, Species: ass1
## Context: liver, Species: glul
## Context: liver, Species: dbp
## Context: liver, Species: pck1
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Batch: 1/100, 0.176584 sec/bs
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: arntl
## Context: liver, Species: pck1
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: arntl
## Context: liver, Species: pck1
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: glul
## Context: liver, Species: arntl
## Context: liver, Species: pck1
## Context: Context: Context: liverliver, Species: ass1
## liver, Species: pck1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## , Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: arntl
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: ass1
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: Context: liver, Species: dbp
## Context: liver, Species: elovl3
## liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: glul
## Context: liver, Species: elovl3
## Context: liver, Species: arntl
## Context: liver, Species: glul
## Context: liver, Species: ass1
## Context: liver, Species: pck1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: arntl
## Context: liver, Species: glul
## Context: liver, Species: ass1
## Context: liver, Species: arntl
## Context: liver, Species: pck1
## Context: liver, Species: dbp
## Context: liver, Species: ass1
## Context: liver, Species: elovl3Context: liver, Species: dbp
## 
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: pck1
## Context: Context: liver, Species: arntl
## liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: ass1
## Context: Context: liver, Species: dbp
## Context: liver, Species: liver, Species: arntl
## dbp
## Context: liver, Species: elovl3
## Context: liver, Species: Context: liver, Species: ass1Context: liver
## , Species: glul
## elovl3
## Context: liver, Species: pck1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: arntl
## Context: liver, Species: glul
## Context: liver, Species: ass1
## Context: liver, Species: pck1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: arntl
## Context: liver, Species: dbp
## Context: liver, Species: ass1
## Context: liver, Species: elovl3
## Context: liver, Species: dbp
## Context: liver, Species: glul
## Context: liver, Species: elovl3
## Context: liver, Species: pck1
## Context: liver, Species: glul
## Context: liver, Species: pck1
## liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: dbp
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: arntl
## Context: liver, Species: dbp
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liverContext: liver, Species: pck1
## , Species: Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: Context: liver, Species: arntl
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: dbp
## Context: liver, Species: elovl3Context: liver, Species: liver
## elovl3
## , Species: pck1
## Context: liver, Species: glul
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: arntl
## Context: liver, Species: elovl3
## Context: liver, Species: ass1
## Context: liver, Species: Context: Context: liverliver, Species: arntl
## glul
## Context: liver, Species: pck1Context: liver, Species: , Species: 
## dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: pck1
## Batch: 10/100, 0.169016 sec/bs
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: arntl
## Context: liver, Species: glul
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: pck1
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: Context: liver, Species: arntl
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: pck1
## liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: ass1
## Context: liver, Species: glul
## Context: liver, Species: arntl
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: pck1
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liverContext: liver, Species: dbp
## Context: liver, Species: arntl
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: ass1Context: , Species: liver, Species: pck1
## arntl
## 
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: arntl
## Context: liver, Species: elovl3
## Context: liver, Species: ass1
## Context: liver, Species: glul
## Context: liver, Species: dbp
## Context: liver, Species: pck1
## Context: liver, Species: elovl3
## Context: liver, Species: arntl
## Context: liver, Species: glul
## Context: liver, Species: ass1Context: liver, Species: pck1
## 
## Context: liver, Species: arntl
## Context: liver, Species: dbp
## Context: liver, Species: ass1
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: dbp
## Context: liver, Species: pck1
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: arntl
## Context: liver, Species: pck1
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: arntl
## Context: liver, Species: elovl3
## Context: liver, Species: ass1
## Context: liver, Species: arntl
## Context: liver, Species: dbp
## Context: Context: liver, Species: glul
## liver, Species: ass1
## Context: liver, Species: elovl3
## Context: liver, Species: dbp
## Context: liver, Species: pck1
## Context: liver, Species: glul
## Context: liver, Species: elovl3
## Context: liver, Species: pck1
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: arntl
## Context: liver, Species: glul
## Context: liver, Species: arntl
## Context: liver, Species: arntl
## Context: liver, Species: Context: liver, Species: ass1
## Context: liver, Species: ass1
## pck1
## Context: liver, Species: dbp
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: pck1
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: arntl
## Context: liver, Species: dbp
## Context: liver, Species: ass1
## Context: liver, Species: elovl3
## Context: liver, Species: arntl
## Context: liver, Species: glul
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: pck1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: elovl3
## Context: liver, Species: pck1
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: Context: liver, Species: ass1
## liver, Species: arntl
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: ass1
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: arntlContext: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## 
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Batch: 20/100, 0.166181 sec/bs
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: elovl3
## Context: liverContext: liver, Species: glul, Species: glul
## 
## Context: liver, Species: pck1
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: arntl
## Context: liver, Species: glul
## Context: liver, Species: ass1
## Context: liver, Species: pck1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: arntl
## Context: Context: liver, Species: ass1
## Context: liver, Species: arntl
## Context: liver, Species: dbp
## liver, Species: glulContext: liver, Species: elovl3
## 
## Context: Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: Context: liver, Species: elovl3
## liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: arntl
## Context: liver, Species: glul
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: arntlContext: liver, Species: pck1
## 
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: arntl
## Context: liver, Species: glul
## Context: liver, Species: ass1
## Context: liver, Species: pck1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: dbp
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: arntl
## arntl
## Context: liver, Species: elovl3
## Context: liver, Species: ass1
## Context: liver, Species: glul
## Context: liver, Species: dbp
## Context: liver, Species: pck1
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: arntl
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Batch: 30/100, 0.160719 sec/bs
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: arntl
## Context: liver, Species: elovl3
## Context: liver, Species: ass1
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: arntl
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: ass1
## Context: liver, Species: pck1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liverContext: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## , Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: Context: liver, Species: arntl
## Context: liver, Species: ass1
## liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: arntl
## Context: liver, Species: dbp
## Context: liver, Species: ass1
## Context: liver, Species: elovl3
## Context: liver, Species: dbp
## Context: liver, Species: glul
## Context: liver, Species: elovl3
## Context: liver, Species: pck1
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: Context: liver, Species: dbp
## Context: liver, Species: elovl3
## liver, Species: pck1
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: ass1
## Context: liver, Species: elovl3
## Context: liver, Species: arntl
## Context: liver, Species: dbp
## Context: liver, Species: glul
## Context: liver, Species: ass1
## Context: liver, Species: elovl3
## Context: liver, Species: dbp
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: elovl3
## Context: liver, Species: pck1
## Context: liver, Species: glul
## Context: liver, Species: arntl
## Context: liver, Species: pck1
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: arntl
## Context: liverContext: liver, Species: ass1
## , Species: pck1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Batch: 40/100, 0.16372 sec/bs
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: arntl
## Context: liver, Species: dbp
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: arntl
## Context: liver, Species: glul
## Context: liver, Species: ass1
## Context: liver, Species: pck1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: arntl
## Context: liver, Species: arntlContext: liverContext: , Species: ass1
## 
## Context: liver, Species: dbp
## Context: liver, Species: ass1
## Context: liver, Species: elovl3
## Context: liver, Species: dbp
## Context: liver, Species: glul
## Context: liver, Species: elovl3
## Context: liver, Species: pck1
## Context: liver, Species: glul
## Context: liver, Species: pck1
## liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: arntl
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: elovl3
## Context: Context: liver, Species: pck1
## Context: liver, Species: glul
## Context: liver, Species: pck1
## liverContext: , Species: dbp
## liver, Species: arntl
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: dbp
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: glul
## Context: liver, Species: pck1Context: liver, Species: dbp
## Context: liver, Species: pck1
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## 
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liverContext: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## , Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: arntl
## Context: liver, Species: elovl3
## Context: liver, Species: ass1
## Context: liver, Species: glul
## Context: liver, Species: dbp
## Context: liver, Species: pck1
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liverContext: liver, Species: ass1
## , Species: arntl
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: ass1
## Context: liver, Species: glul
## Context: liver, Species: Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## pck1
## Batch: 50/100, 0.165886 sec/bs
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: arntl
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: elovl3
## Context: liver, Species: pck1
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: arntl
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: arntl
## Context: liver, Species: pck1
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: arntl
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: ass1
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: dbp
## Context: liver, Species: pck1
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: pck1
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: arntl
## Context: liver, Species: pck1
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: arntl
## Context: liverContext: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3, Species: Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## glul
## Context: liver, Species: pck1
## 
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: arntl
## Context: liver, Species: glul
## Context: liver, Species: ass1
## Context: liver, Species: pck1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: arntl
## Context: liver, Species: glul
## Context: liver, Species: ass1
## Context: liver, Species: pck1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: arntl
## Context: Context: liver, Species: pck1
## liver, Species: arntl
## Context: liver, Species: ass1
## Context: Context: liver, Species: dbp
## liver, Species: ass1
## Context: liver, Species: elovl3
## Context: liver, Species: dbp
## Context: liver, Species: glul
## Context: liver, Species: elovl3
## Context: liver, Species: pck1
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: Context: liver, Species: dbp
## Context: liver, Species: elovl3
## liver, Species: arntl
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: ass1
## Context: liver, Species: arntl
## Context: liver, Species: dbp
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: glul
## Context: liver, Species: Context: pck1
## liver, Species: arntl
## Context: liver, Species: pck1
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## 
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Batch: 60/100, 0.16429 sec/bs
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: ass1
## Context: liver, Species: glul
## Context: liver, Species: dbp
## Context: liver, Species: pck1
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: arntl
## Context: liverContext: liver, Species: elovl3
## , Species: dbp
## Context: liver, Species: glul
## Context: liver, Species: elovl3
## Context: liver, Species: ass1
## Context: liver, Species: glul
## Context: liver, Species: Context: liverdbp
## , Species: pck1
## Context: liver, Species: elovl3
## Context: liver, Species: pck1
## Context: liver, Species: glul
## Context: Context: liver, Species: arntl
## liver, Species: pck1
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liverContext: liver, Species: glul
## Context: liver, Species: pck1
## , Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: arntl
## Context: liver, Species: glul
## Context: liver, Species: ass1
## Context: liver, Species: pck1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: Context: liver, Species: glul
## liver, Species: arntl
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: elovl3
## Context: liver, Species: glulContext: 
## liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: arntl
## Context: liver, Species: glul
## Context: liver, Species: ass1
## Context: liver, Species: pck1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Batch: 70/100, 0.166005 sec/bs
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: arntl
## Context: liver, Species: elovl3
## Context: liverContext: liver, Species: glul
## Context: liver, Species: pck1
## , Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: arntl
## Context: liver, Species: arntl
## Context: liver, Species: dbp
## Context: liver, Species: ass1
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: pck1
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: arntl
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: ass1
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: elovl3
## Context: liver, Species: dbp
## Context: liver, Species: glul
## Context: liver, Species: elovl3
## Context: liver, Species: pck1
## Context: Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## liver, Species: glul
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: arntl
## Context: Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: Context: liver, Species: arntlliver, Species: arntlContext: liver, Species: elovl3
## 
## Context: liver, Species: glul
## Context: liver, Species: ass1
## Context: liver, Species: pck1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## 
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: arntl
## Context: liver, Species: elovl3
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: glul
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1Context: liver, Species: pck1
## 
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: Context: liver, Species: ass1
## Context: liver, Species: dbp
## arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## liver, Species: elovl3
## Context: liver, Species: dbp
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: arntl
## Context: liver, Species: pck1
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: arntl
## Context: liver, Species: dbp
## Context: liver, Species: ass1
## Context: liver, Species: elovl3
## Context: liver, Species: dbp
## Context: liver, Species: glul
## Context: liver, Species: elovl3
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: glul
## Context: liver, Species: dbp
## Context: liver, Species: pck1
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: arntl
## Context: liver, Species: glul
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: pck1
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: arntl
## Context: liver, Species: pck1
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: glul
## Context: liver, Species: dbp
## Context: liver, Species: pck1
## Context: liver, Species: elovl3
## Context: liver, Species: arntl
## Context: liverContext: liver, Species: ass1
## , Species: glul
## Context: liver, Species: dbp
## Context: liver, Species: pck1
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Batch: 80/100, 0.191563 sec/bs
## Context: Context: liverliver, Species: arntlContext: 
## , Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: dbp
## liver, Species: arntl
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: ass1
## Context: liver, Species: pck1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: Context: liver, Species: arntl
## Context: liver, Species: ass1
## liver, Species: arntl
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: arntl
## Context: liver, Species: elovl3
## Context: liver, Species: ass1
## Context: liver, Species: Context: glulliver, Species: dbpContext: 
## liver, Species: Context: arntl
## liver, Species: glul
## Context: liver, Species: elovl3
## Context: liver, Species: ass1
## 
## Context: liver, Species: glul
## Context: liver, Species: dbp
## Context: liver, Species: pck1
## Context: liver, Species: pck1
## Context: liver, Species: elovl3
## Context: liver, Species: pck1
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: Context: liverliver, Species: arntlContext: 
## liver, Species: arntl
## , Species: Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: ass1
## pck1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liverContext: liver, Species: glul
## Context: liver, Species: elovl3
## Context: liver, Species: pck1
## Context: liver, Species: glul
## Context: liver, Species: pck1
## , Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: arntl
## Context: liver, Species: dbp
## Context: liver, Species: ass1
## Context: liver, Species: arntl
## Context: liver, Species: elovl3
## Context: Context: liver, Species: glul
## Context: liver, Species: dbp
## Context: liver, Species: pck1
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: arntl
## Context: liver, Species: pck1
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: arntl
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: Context: liver, Species: pck1
## liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: arntl
## Context: liver, Species: Context: liver, Species: pck1
## ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liverContext: liver, Species: arntl
## , Species: pck1
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: arntl
## Context: liver, Species: Context: liver, Species: pck1
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: arntl
## Context: liver, Species: elovl3
## Context: Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: arntl
## Context: liver, Species: glul
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: pck1
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: Context: liver, Species: arntl
## elovl3
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: arntl
## Context: liver, Species: elovl3
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: glulContext: liver, Species: glul
## Context: liver, Species: elovl3
## Context: liver, Species: pck1
## Context: liver, Species: glul
## Context: liver, Species: pck1
## 
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Batch: 90/100, 0.15588 sec/bs
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: arntl
## Context: liver, Species: pck1
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: arntl
## Context: liver, Species: pck1
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: Context: liver, Species: elovl3
## liver, Species: arntl
## Context: liver, Species: glul
## Context: liver, Species: ass1
## Context: liver, Species: pck1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: arntl
## Context: liver, Species: glul
## Context: liver, Species: ass1
## Context: liver, Species: pck1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: arntl
## Context: liver, Species: pck1
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: arntl
## Context: liver, Species: dbp
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: Context: liver, Species: elovl3
## liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: dbp
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: arntl
## Context: liver, Species: dbp
## Context: liver, Species: ass1
## Context: liver, Species: elovl3
## Context: liver, Species: dbp
## Context: liver, Species: glul
## Context: liverContext: liver, Species: pck1
## , Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: arntl
## Context: liver, Species: elovl3
## Context: liver, Species: ass1
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: elovl3
## Context: liver, Species: dbp
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## Context: liver, Species: arntl
## Context: liver, Species: ass1
## Context: liver, Species: dbp
## Context: liver, Species: elovl3
## Context: liver, Species: glul
## Context: liver, Species: pck1
## All complete!
## 
## Bootstrap simulation complete... 
## Bootstrap run time (total), minutes: 2.899
## Bootstrap run time (per sample), seconds: 0.174
## Bootstrap run time (per sample, per thread), seconds: 1.739
## 
## Setting full-data fit as parameters... 
## Checking feasibility of provided parameters
## ... no tpoints below buffer
## ... no NAN rates predicted
## ... no negative rates predicted
## Provided parameters are feasible
## Initial boundary distance (want > 0): 0.378776
## 
## Running stats on simulation results
## ----------------------------------------
## 
## Grabbing sample results, only resamples with converged fit... 
## Grabbing parameter values... 
## Computing 95% confidence intervals... 
## Estimating p-values from resampled parameters... 
## 
## Recommended resample size for alpha = 0.05, 108 tests
## with bootstrapping/MCMC: 2160
## Actual resample size: 1001
## 
## Stat summary (head only):
## ------------------------------
##                           parameter    estimate    CI.low   CI.high     p.value p.value.adj    alpha.adj significance
## 1  baseline_liver_Rt_arntl_Tns/Blk1  2.52351157  2.147938 2.8419666          NA          NA           NA             
## 2  beta_Rt_liver_arntl_6_X_Tns/Blk1 -1.42987696 -2.578113 3.1579983 0.004995005  0.33466533 0.0007462687           ns
## 3 beta_Rt_liver_arntl_12_X_Tns/Blk1 -0.03715176 -1.591022 0.8591341 0.911088911  3.64435564 0.0125000000           ns
## 4 beta_Rt_liver_arntl_18_X_Tns/Blk1  0.13107595 -0.664336 1.8067587 0.742257742  6.68031968 0.0055555556           ns
## 5  baseline_liver_Rt_arntl_Tns/Blk2  1.96922136  1.593244 2.2705854          NA          NA           NA             
## 6  beta_Rt_liver_arntl_6_X_Tns/Blk2 -0.95957998 -1.478458 0.6556153 0.000999001  0.07592408 0.0006578947           ns
## ----
## 
## Computing 95% CI for predicated values by bin
## ----------------------------------------
## 
## Grabbing sample results, only resamples with converged fit... 
## Computing predicted values for each sampled parameter set... 
## Computing 95% CIs... 
## 
## Analyzing residuals
## ----------------------------------------
## 
## Computing residuals... 
## Making masks... 
## Making plots and saving stats... 
## 
## Log-residual summary by grouping variables (head only):
## ------------------------------
##          group      mean        sd  variance
## 1          all 0.3761585 0.4347535 0.1890106
## 2 ran_lvl_none 0.3469852 0.3374680 0.1138847
## 3    ran_lvl_1 0.4181383 0.4768411 0.2273775
## 4   ran_lvl_10 0.4131620 0.5134598 0.2636409
## 5    ran_lvl_2 0.3451371 0.4303134 0.1851696
## 6    ran_lvl_3 0.4122882 0.5838509 0.3408819
## ----
## 
## Making effect parameter distribution plots... 
## Making rate-count plots... 
## Making time series plots... 
## Making parameter plots... 
## Making parameter plots... 
## Making parameter plots... 
## Making parameter plots... 
## Making parameter plots... 
## Making parameter plots...

Examining results

The wisp() function produces both a rate-count plot with space along the x-axis and a time-series plot with time along the x-axis. By examining the plots of the the model fit for each gene, we can assess how well wisp has captured zonation and temporal rhythm. The below plots align with the expectations in the above table, and are a near match for the plots produced by the bespoke model of Droin et al. (2021) and shown in figure 1. (However, note that the colors used in the plots here differ from those used in the paper figure.)

Zonated genes

To begin, consider GLUL and ASS1, which are expected to be primarily zonated, with GLUL being higher in the central region and ASS1 being higher in the portal region. Their respective spatial gradients are easy to see in the rate-count plot:

plt_glul <- radial.model[["plots"]][["ratecount"]][["plot_pred.log_context_liver_fixEff_glul"]]
plt_ass1 <- radial.model[["plots"]][["ratecount"]][["plot_pred.log_context_liver_fixEff_ass1"]]
g <- arrangeGrob(plt_glul, plt_ass1, ncol = 2)  
grid.draw(g)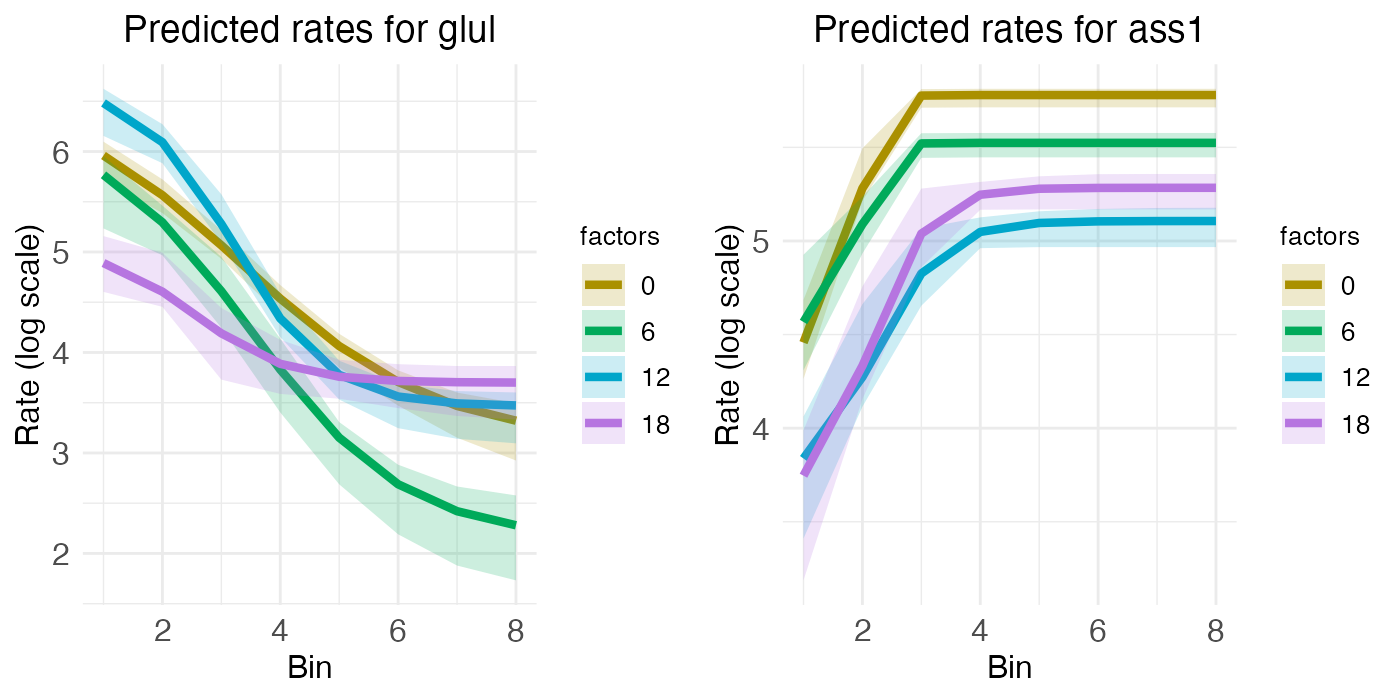

While the rate-count plots make clear the spatial gradients of GLUL and ASS1, temporal information can only be read off implicitly. For ASS1, we seem to see a slight decrease in gene expression over the day, from ZT0 to ZT18. For GLUL, expression seems constant across the day, except perhaps for some minor interaction between zone and time that has the central region decreasing in expression as the portal region increases. These temporal patterns can be seen more clearly by looking at the time-series plots.

plt_glul <- radial.model[["plots"]][["timeseries"]][["plot_pred.log_context_liver_timeseries_glul"]]
plt_ass1 <- radial.model[["plots"]][["timeseries"]][["plot_pred.log_context_liver_timeseries_ass1"]]
g <- arrangeGrob(plt_glul, plt_ass1, ncol = 2)  
grid.draw(g)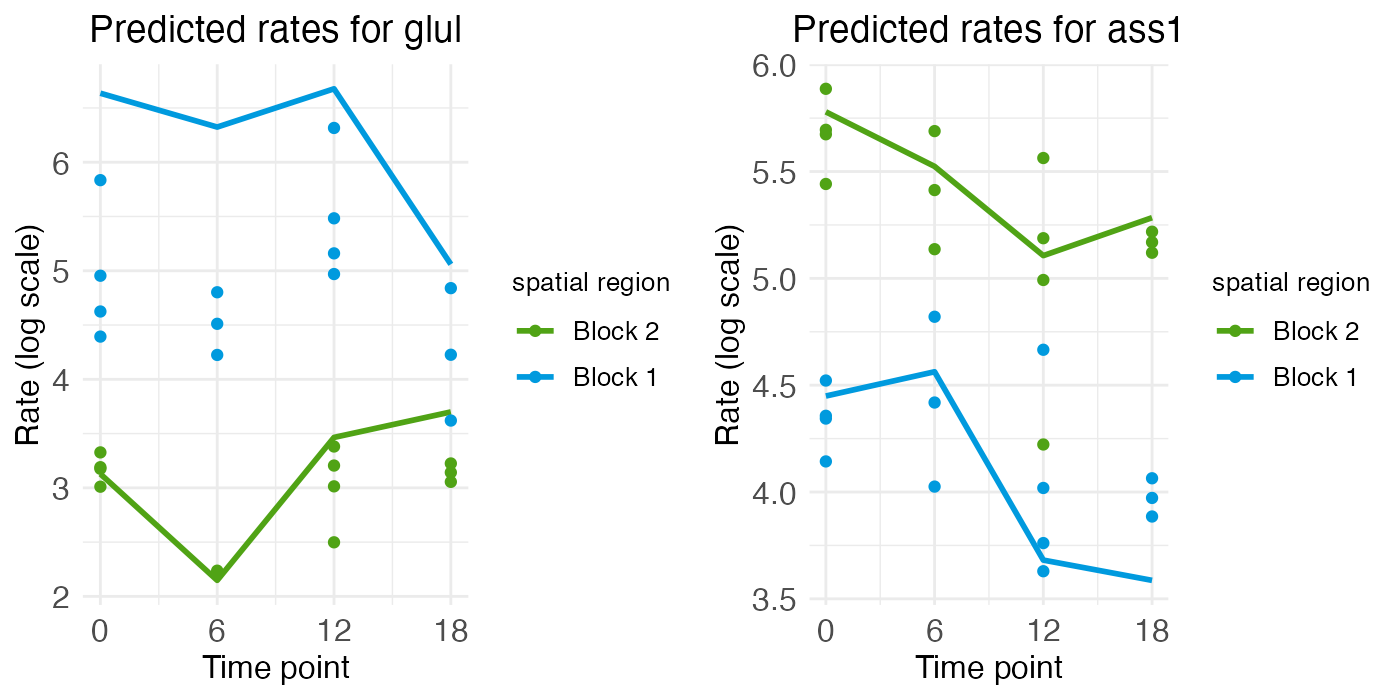

The time-series plot for ASS1 shows some variation over time, but the magnitude of that variation is small compared to the difference in expression level between the blocks (i.e., over space). The same holds true for GLUL, although again we see the more portal region (block 2) seeming to increase in expression while the more central region (block 1) decreases.

Rhythmic genes

For the two rhythmic genes, the spatial rate-count plots show two times with relatively low and flat expression, along with two times with relatively high expression, although the central region of ARNTL shows a bit of a spatial gradient. For the portal region of ARNTL, ZT0 and ZT18 are elevated (yellow and purple), while for DBP it’s ZT6 and ZT12 (green and blue) that are elevated.

plt_arntl <- radial.model[["plots"]][["ratecount"]][["plot_pred.log_context_liver_fixEff_arntl"]]
plt_dbp <- radial.model[["plots"]][["ratecount"]][["plot_pred.log_context_liver_fixEff_dbp"]]
g <- arrangeGrob(plt_arntl, plt_dbp, ncol = 2)  
grid.draw(g)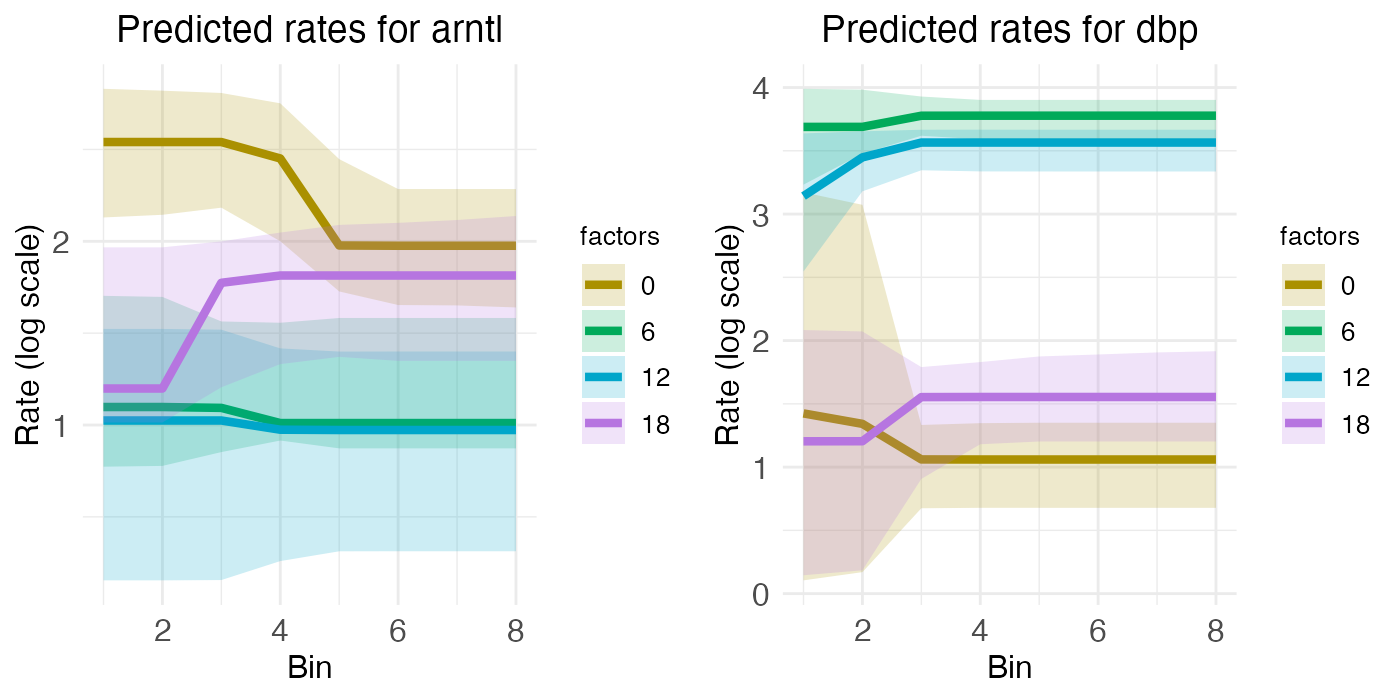

These temporal dynamics are made more clear in the time-series plots, which clearly show the mid-ZT dip in ARNTL and the mid-ZT bump in DBP.

plt_arntl <- radial.model[["plots"]][["timeseries"]][["plot_pred.log_context_liver_timeseries_arntl"]]
plt_dbp <- radial.model[["plots"]][["timeseries"]][["plot_pred.log_context_liver_timeseries_dbp"]]
g <- arrangeGrob(plt_arntl, plt_dbp, ncol = 2)  
grid.draw(g)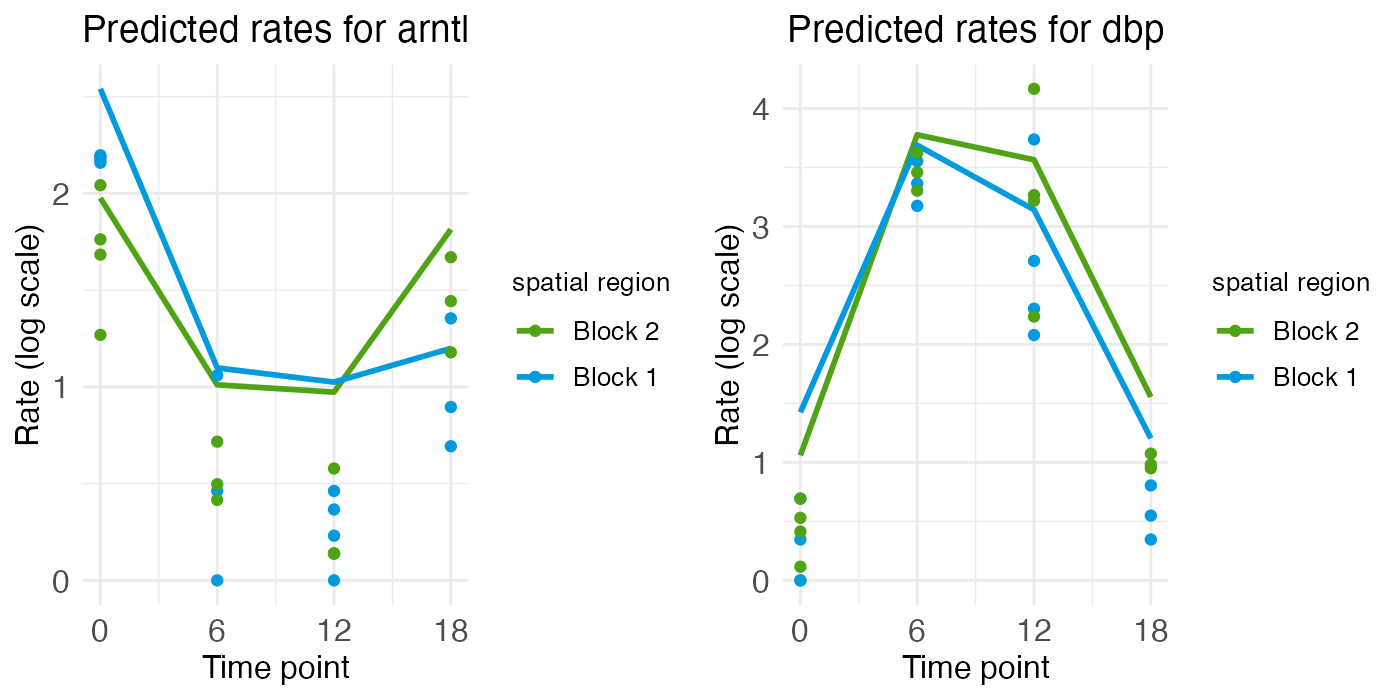

Zonated and rhythmic genes

Finally, we have ELOVL3 and PCK1, two genes with both spatial zonation and temporal rhythm. Spatially, ELOVL3 has the same profile as GLUL. Both are expressed more in the central region. PCK1, on the other hand, is expressed more in the portal region, just like ASS1.

plt_elovl3 <- radial.model[["plots"]][["ratecount"]][["plot_pred.log_context_liver_fixEff_elovl3"]]
plt_pck1 <- radial.model[["plots"]][["ratecount"]][["plot_pred.log_context_liver_fixEff_pck1"]]
g <- arrangeGrob(plt_elovl3, plt_pck1, ncol = 2)  
grid.draw(g)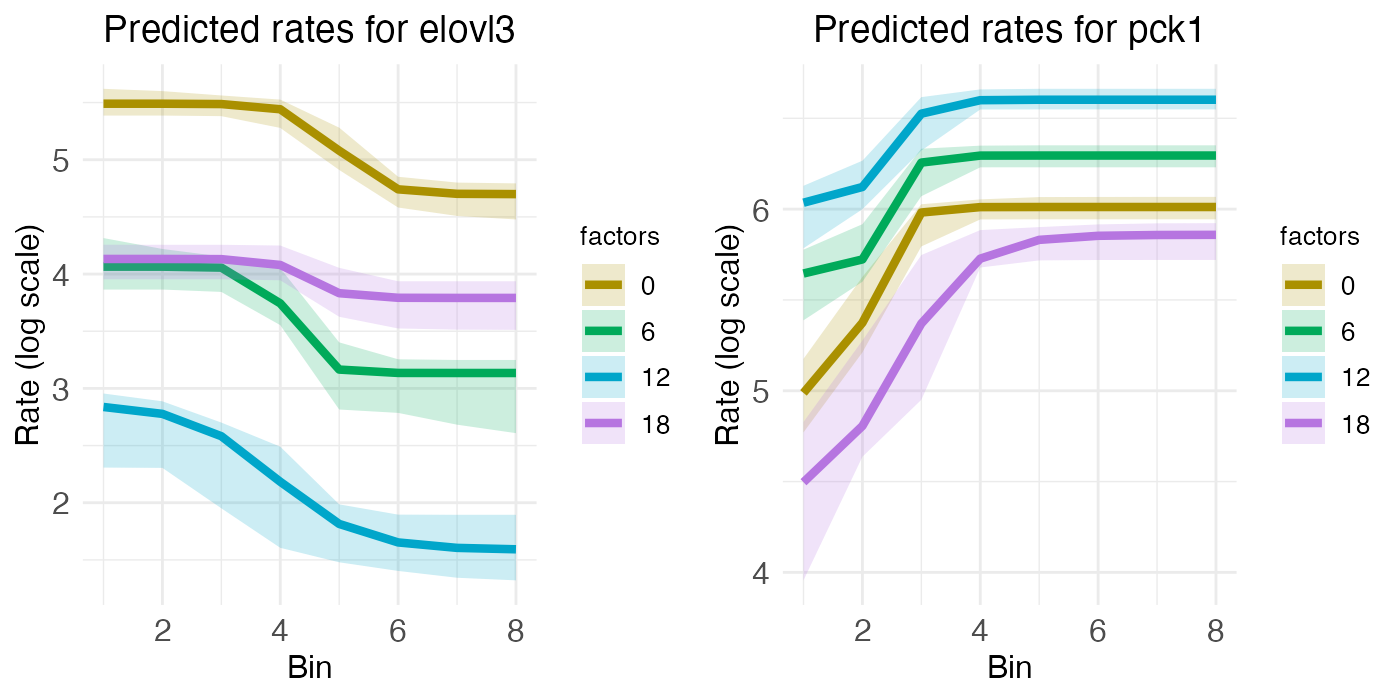

However, unlike GLUL and PCK1, ELOVL3 and PCK1 have notable temporal rhythm. ELOVL3 is similar to ARNTL, with a mid-ZT dip. PCK1 is similar to DBP, with a mid-ZT bump.

plt_elovl3 <- radial.model[["plots"]][["timeseries"]][["plot_pred.log_context_liver_timeseries_elovl3"]]
plt_pck1 <- radial.model[["plots"]][["timeseries"]][["plot_pred.log_context_liver_timeseries_pck1"]]
g <- arrangeGrob(plt_elovl3, plt_pck1, ncol = 2)  
grid.draw(g)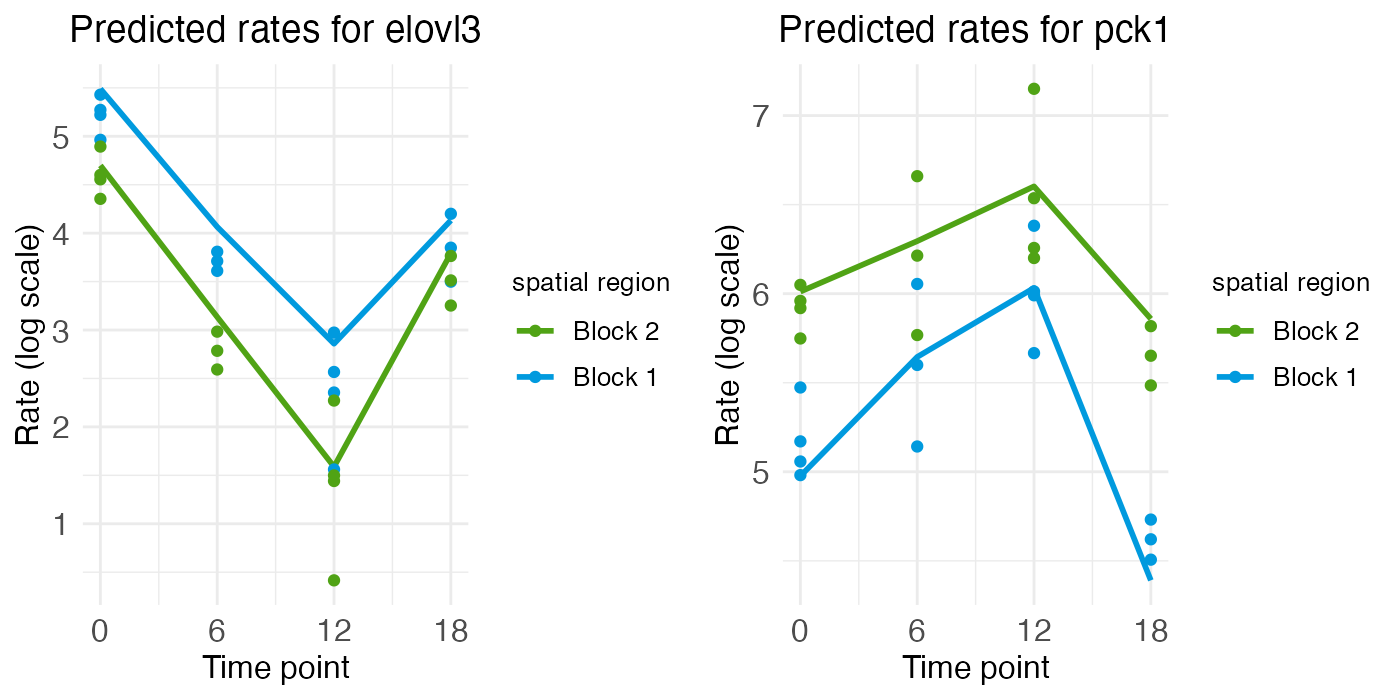

Advantages of wisp

The advantage of using a wisp is that it eliminates the need to build a bespoke model, both in the first place and for extending the analysis. The approach of Droin et al. depends on the assumption that liver zonation is well-modeled by second-degree polynomials and that temporal effects on this zonation are rhythmic. If we want to extend this analysis to test for other potential FSEs besides temporal rhythm, such as gene mutation, drug treatment, or disease state, we would need to build new models for each of these effects. Wisp, on the other hand, can model other fixed-effects directly, without needing to change the model structure. In addition, wisp is not limited to the assumption that the random effect is linear.